Ce billet de blogue est coécrit par mon étudiant au doctorat, Edward J. Hu.
La mise à l’échelle semble très bien fonctionner.
Nous devons faire preuve de prudence lorsque nous explorons des orientations de recherche qui intègrent directement les connaissances dans les systèmes d’IA aux dépens de l’extensibilité à plus grande échelle. En fait, même la nature développe l’intelligence à partir de réseaux neuronaux biologiques à grande échelle.
Toutefois, les systèmes à grande échelle actuels présentent encore d’importantes erreurs factuelles et un comportement imprévisible lorsqu’ils sont déployés. Même s’il se peut que ces erreurs s’améliorent avec des solutions à court terme comme davantage de filtres, une meilleure extraction d’informations pertinentes et des invites plus intelligentes, ces systèmes ne pensent pas comme les humains, comme l’indique la neuroscience cognitive, en particulier, la théorie de l’espace de travail global [Baars, 1988] et ses descendants. Il est dur de confier des tâches importantes à un tel système que nous comprenons peu.
À notre avis, il est peu probable qu’une mise à l’échelle plus approfondie résolve ces questions de fiabilité. Le prix de mise à l’échelle inverse montre que des modèles plus grands obtiennent de moins bons résultats par rapport à de nombreuses tâches bien spécifiées. Si nous croyions que les modèles plus grands seraient nécessairement plus fiables, tout signe de mise à l’échelle « inverse » devrait être alarmant. Un grand nombre de ces tâches font appel à des formes de raisonnement, suggérant que pour atteindre un raisonnement solide de niveau humain, nous avons besoin de biais inductifs supplémentaires.
Ce billet de blogue décrit les orientations de recherche à long terme qui tirent parti des biais inductifs et de la mise à l’échelle. Nous soulignerons ce qui, à notre avis, est la source du problème avec la technologie de pointe actuelle et définirons les solutions possibles. Tout d’abord, nous devons nous demander ce qu’est le raisonnement.
Raisonnement = connaissance + inférence
Le raisonnement, ou la pensée, est le processus qui consiste à poser des questions et à y répondre en utilisant une source de connaissances.
Le raisonnement humain exige de générer un petit nombre d’étapes intermédiaires, c.-à-d., des pensées, chacune d’entre elles combinant un très petit nombre de fragments de connaissance de manière cohérente [Baars, 1988]. Le nom technique générique pour désigner le fait de « répondre aux questions » dans l’apprentissage automatique probabiliste est inférence. Techniquement, faire de l’inférence probabiliste veut dire trouver des modes de la distribution conditionnelle P(solution | question, connaissance). Une « solution » ou réponse à la question peut prendre ici la forme d’un objet compositionnel arbitraire. Cela peut comprendre la réponse explicite à la question et les explications hypothétiques sur le lien entre la question et la réponse. Les séquences de langage naturel sont habituellement une réflexion de tels objets compositionnels, comme les arbres d’analyse sémantique, qui sont dans nos esprits lorsqu’une réponse apparaît et qui expliquent en partie la phrase, nous aidant à répondre à la question sur le sujet. Comme nous le verrons ultérieurement, pour bien raisonner, nous avons besoin d’avoir 1) un bon modèle du monde et 2) un moteur d’inférence puissant pour trouver des solutions compatibles avec le modèle du monde.
C’est là qu’apparaissent différents compromis informatiques et statistiques.
D’un côté, selon le rasoir d’Occam, notre modèle du monde cherche des fragments de connaissance minimalement suffisants pour expliquer les données observées. Il devrait être compact en ce qui a trait au nombre de bits qu’il encode et maximiser le caractère réutilisable des fragments de connaissance afin qu’il puisse bien généraliser face aux situations inédites. Par exemple, dans le jeu de Go, le modèle du monde devrait représenter les règles. Si elles ne sont pas données au départ, il devrait être possible de les apprendre à partir d’exemples de parties jouées de façon à pouvoir expliquer de nouvelles parties. Ce modèle du monde n’a pas besoin d’être dans une forme explicite comme un graphe de connaissances. Il peut prendre la forme d’un modèle basé sur l’énergie E(question, solution) paramétré par un réseau neuronal qui évalue la compatibilité entre une question et une solution et, possiblement, une connaissance plus formelle et verbalisable du type que nous utilisons en sciences, en mathématiques, dans les bases de données ou Wikipédia. Néanmoins, la capacité effective de ce réseau neuronal est limitée par la quantité de données à notre disposition – un réseau neuronal trop grand peut facilement surapprendre si ses paramètres sont pleinement exploités.
D’autre part, un moteur d’inférence entraîné peut amortir le coût computationnel de la recherche dans un grand espace de solution; il peut apprendre à fournir rapidement des réponses qui sont bonnes et qu’une méthode de recherche explicite comme les méthodes de Monte-Carlo par chaîne de Markov, d’IA classique ou d’optimisation, pourrait autrement fournir pour un coût de calcul bien plus élevé. Ce moteur d’inférence doit être très puissant – l’inférence exacte, qui épuise toutes les configurations combinatoires de fragments de connaissance, requiert une puissance de calcul exponentielle, même si le problème est spécifié par une quantité modeste de connaissances. Pensez à la façon dont quelques règles simples, comme dans le jeu de Go requièrent un très grand réseau neuronal afin d’effectuer une bonne inférence, c.-à-d., jouer au niveau des champions. En d’autres termes, l’inférence approximative est le point fort de la mise à l’échelle : plus le modèle est grand, plus l’approximation est précise. Toutefois, un grand réseau neuronal a un prix en matière du nombre d’exemples requis pour alimenter la machine et assurer sa précision.
En matière de raisonnement fiable, le fait que le modèle du monde et le moteur d’inférence sont une seule et même chose constitue le talon d’Achille des grands modèles de langage actuels. Un réseau neuronal monolithique entraîné de bout en bout sur les données d’entraînement fournies pour effectuer l’inférence souhaitée peut avoir de la difficulté à atteindre en même temps les deux objectifs finaux (représentation des connaissances et inférence). Un moteur d’inférence puissant qui contient implicitement la connaissance peut facilement découvrir un modèle du monde implicite trop compliqué. Vu sous cet angle, il est moins surprenant que les grands modèles de langage actuels ne parviennent pas toujours à généraliser de la même manière que les humains face à de nouvelles observations.
Le reste du billet de blogue décrit ce à quoi peuvent ressembler un modèle du monde idéal et un moteur d’inférence idéal. Commençons par les propriétés d’un modèle du monde idéal.
Le modèle du monde idéal
Le modèle mental du monde des humains nous permet de généraliser rapidement face aux nouvelles situations en utilisant très peu de données pour s’y adapter, comme conduire de l’autre côté de la route en raison d’un règlement de circulation modifié ou résoudre de nouveaux casse-têtes de codage.
Pour ce faire, nous réutilisons et adaptons des fragments de connaissances existants, similaire aux principes de modularité et de réutilisabilité en programmation. Nous nous fions également aux langages naturels et à d’autres symboles abstraits pour organiser la connaissance et les pensées et pour les communiquer sous des formes compactes, p. ex. avec des équations ou des définitions du dictionnaire. En fait, notre mémoire de travail a une capacité si limitée et elle ne peut retenir qu’une petite série distincte de concepts [Dehaene et autres, 2022]. Ce goulot d’étranglement biologique, au cœur de la théorie de l’espace de travail global [Baars, 1988] de la neuroscience cognitive, entraîne un modèle du monde compact et modulaire [Goyal et Bengio 2022]. Les neurosciences ont démontré que notre mémoire de travail condense l’information observée en exploitant sa structure abstraite (comme les répétitions) de la même manière que définir un nouveau concept nous permet de l’utiliser d’une façon qui nécessite moins de bits au total, si le concept est réutilisé plusieurs fois, et cette capacité peut expliquer la raison pour laquelle nous inventons de nouvelles abstractions différemment des autres animaux [Dehaene et autres, 2022]. Avec l’aide des langages naturels, nous inventons constamment de nouvelles abstractions et définitions afin de mieux condenser et comprendre le monde.
En plus de la modularité, la notion d’incertitude est cruciale. Généralement, de nombreux modèles du monde peuvent être compatibles avec une quantité finie de données . Le fait de se fier à un seul modèle parmi ceux qui sont compatibles avec les données peut produire des résultats d’inférence qui se trompent tout en étant confiants dans la réponse fournie, ce qui peut mener à des décisions dangereuses. Les humains sont plutôt capables d’évaluer leur propre degré d’incertitude par rapport à une déclaration, ne serait-ce que grossièrement; ils gèrent donc les risques de manière plus appropriée. Prendre conscience de sa propre incertitude par rapport à ses connaissances est également un élément essentiel de l’acquisition efficace de connaissance [Jain et autres, 2023]. Par exemple, nous pouvons recueillir davantage de données d’entraînement pour les scénarios présentant une incertitude élevée (ce qui est la source de la curiosité) et le fait d’utiliser de bonnes estimations d’incertitude nous permet même d’automatiser la mise au point des expériences dans la recherche scientifique.
Pour terminer, le modèle du monde devrait tirer parti du pouvoir de généralisation hors distribution offert par la modélisation des relations causales. La causalité joue un rôle important dans le raisonnement humain. Par exemple, nous savons qu’en raison de la gravité, les objets tombent et qu’en raison de la pluie, les routes sont mouillées, mais l’inverse n’est pas vrai, car rendre les routes mouillées n’entraîne pas de pluie. Un modèle causal peut être compris comme une famille de distributions exponentiellement grande indexée par un choix d’intervention, où une intervention fixe ou change quelques variables. Dans le cas du raisonnement humain, une intervention correspond à l’action d’un agent. Une telle connaissance causale nous aide à généraliser face à une distribution inédite correspondant à une nouvelle intervention. Cela nous permet également de décider comment intervenir dans le monde afin d’atteindre les objectifs souhaités et aussi de raisonner de manière contrefactuelle en répondant à la question « qu’est-ce qui aurait pu se produire si j’avais fait les choses différemment? », un outil utile pour décider comment on aurait dû agir et qui peut s’avérer efficace pour l’apprentissage des dépendances causales à long terme [Kemp et autres, 2015].
L’apprentissage automatique basé sur un modèle avec de grands réseaux profonds comme moteurs d’inférence amortis
Penser, c’est chercher des idées ou des solutions.
L’inférence consiste à trouver des aiguilles dans une botte de foin. La distribution P(solution | question, connaissance) favorise habituellement un tout petit nombre de modes (régions de probabilité élevée dans un espace de solution) provenant d’un espace exponentiellement grand de solutions possibles. L’inférence classique, y compris les méthodes de Monte-Carlo par chaîne de Markov, est basée sur une recherche basée sur la force brute de calcul : essayer un grand nombre de solutions, souvent en améliorant celles trouvées précédemment. Il s’agit d’une méthode très dispendieuse lors de l’exécution et pas pratique du point de vue d’un animal faisant face à un danger imminent. À la place, le coût de calcul de l’inférence peut être amorti, signifiant qu’on échange une procédure d’entraînement au coût de calcul élevé contre une inférence rapide au moment de l’exécution – plus le moteur d’inférence est utilisé et ajusté avec précision, plus il s’améliore. Par exemple, une scientifique peut pratiquer son habileté à résoudre des problèmes à l’université pendant deux décennies tout en étant capable de répondre de plus en plus rapidement à des questions difficiles dans son domaine. Une approche non amortie ne requiert pas ces années d’études, mais plutôt de trouver les réponses à chaque nouvelle question à partir de rien, grâce à un grand nombre de calculs. Cette approche ne passera pas à l’échelle pour les problèmes difficiles. Cela exclut l’inférence basée sur la simulation comme les méthodes de Monte-Carlo par chaîne de Markov ainsi que les méthodes de recherche d’IA classique comme A*. Entre-temps, cette éducation d’IA, obtenue par apprentissage amorti, devrait se prêter à une optimisation stochastique efficace basée sur le gradient pour tirer parti des avancées en apprentissage profond des deux dernières décennies.
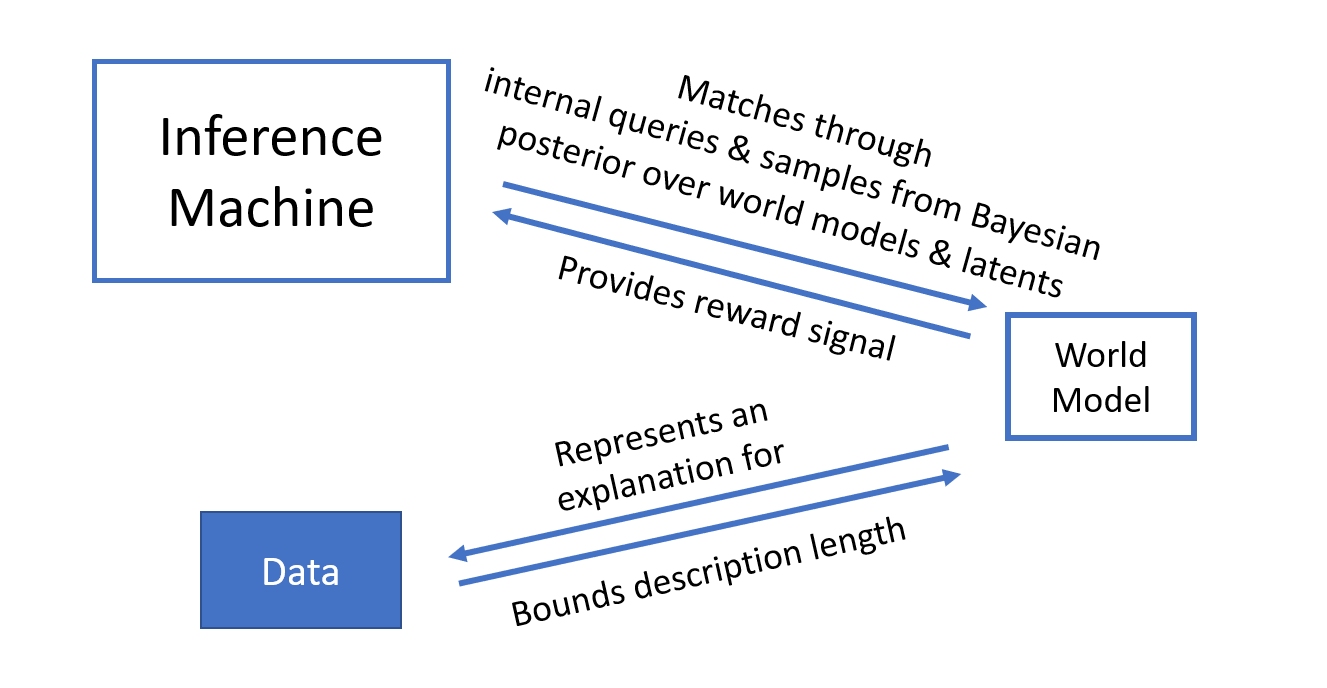
Nous proposons de raviver une ancienne idée en sciences et en apprentissage automatique : séparer le modèle du monde et le moteur d’inférence, mais exploiter l’apprentissage automatique moderne pour entraîner un très grand moteur d’inférence amorti. Comment doit-il être entraîné? Le moteur d’inférence amorti devrait être cohérent avec le modèle du monde. Si l’on demande à quelqu’un « comment faire une brioche moelleuse? », la réponse devrait être basée sur les fragments de connaissance se rapportant à la pâtisserie combinés de manière cohérente. Cette cohérence peut être encouragée par une procédure d’entraînement qui questionne le modèle du monde et quantifie la cohérence du résultat de l’inférence avec les fragments de connaissance pertinents. Cela présente un autre avantage : si nous pouvons nous permettre d’effectuer de nombreux calculs utilisés pour entraîner le moteur d’inférence avec des questions au modèle du monde, nous ne surapprendrons pas facilement, même si le moteur d’inférence amorti est très gros. De nombreuses questions peuvent être posées et utilisées de manière combinatoire pour entraîner le moteur d’inférence amorti : la quantité de « faux » exemples utilisés pour entraîner le moteur d’inférence est dorénavant sans bornes, car ces « faux exemples » ne sont pas limités par les données réelles, mais ils se manifestent sous la forme de questions internes, et leur nombre n’est limité que par notre capacité informatique. Par conséquent, nous pouvons tirer pleinement parti du pouvoir des réseaux neuronaux pour le moteur d’inférence sans craindre un surapprentissage.
En outre, il existe souvent plus d’une solution à une question. Le moteur d’inférence devrait être capable de modéliser une distribution plurimodale par rapport aux réponses, plutôt que se concentrer sur une seule réponse, on obtient une distribution sur les réponses qui sont compatibles avec le modèle du monde et avec la question. Cela va de pair avec la notion d’incertitude dans le modèle du monde – nous avons souvent de nombreuses hypothèses de fonctionnement du monde. En fait, la même machinerie d’inférence probabiliste peut, de manière bayésienne, prédire la distribution sur les modèles du monde compatibles avec les données [Deleu et autres, UAI’22]. Ensuite, les aspects du modèle comportant une incertitude élevée peuvent être rendus moins incertains grâce à l’acquisition des données pertinentes [Jain et autres, 2023].
Pour terminer, le moteur d’inférence peut explorer le grand espace de solution de manière efficace. Pour représenter les nombreux candidats de manière combinatoire dans l’espace de solution, le moteur d’inférence peut trouver une solution par l’entremise d’une séquence d’étapes stochastiques, chacune étant choisie à partir d’un espace d’action plus petit. Par exemple, nous pouvons construire des molécules en choisissant un emplacement de façon répétée et en ajoutant un atome à la fois. Chaque action est tirée d’une série limitée, mais leur composition à travers plusieurs étapes permet de représenter une distribution arbitrairement riche par rapport aux molécules. Lorsqu’il est entraîné sur diverses questions et solutions, le moteur d’inférence peut mélanger ou apparier les étapes déjà vues et faire une estimation éclairée afin d’arriver à des solutions précédemment inédites, p. ex. en recombinant des groupes fonctionnels pour former de nouvelles molécules organiques. Cette forme de généralisation en exploitant les régularités sous-jacentes dans l’espace de solution est au cœur de la réussite de l’apprentissage profond moderne.
Au-delà de la mise à l’échelle
Selon Daniel Kahneman, notre cerveau comprend un système 1 caractérisé par une pensée rapide et associative et un système 2, correspondant à une cognition lente, séquentielle (une chaîne de pensées) et mûrement réfléchie. De nombreuses personnes comparent les modèles de langage basés sur l’apprentissage profond au système 1 et posent comme principe qu’une architecture future du système 2 gérera le raisonnement fiable [Goyal et Bengio 2022]. Toutefois, il se peut qu’un réseau neuronal basé uniquement sur le système 2 ne soit pas pratique, pour la même raison que l’IA symbolique classique a échouée – il doit aussi disposer d’un moteur d’inférence puissant, pour une inférence rapide permettant de répondre à une nouvelle question à la volée ainsi que pour l’entraînement du modèle du monde lui-même et déduire des explications pour les données observées. En effet, notre cerveau est rempli de réseaux neuronaux localement denses, à la manière du système 1, et le système 2 peut organiser simplement le calcul et l’entraînement du premier afin d’obtenir une cohérence entre un moteur d’inférence amorti puissant et un modèle du monde représenté implicitement, mais compact et modulaire.
Par quels moyens crédibles peut-on aller au-delà de la mise à l’échelle des grands modèles de langage actuels?
À court terme, il se peut que, d’une manière ou d’une autre, nous encouragions le modèle du monde dans les modèles de langage à être modulaire et de modéliser l’incertitude et la causalité; cela requiert plus de recherche sur la compréhension du fonctionnement des modèles de langage et la manière dont leur machinerie pourrait être mise à profit pour générer non seulement des actions externes, mais aussi une voix intérieure qui peut être perçue comme une variable latente qui explique en partie les séquences de mots externes précédentes ou à venir.
À long terme, nous devrions séparer le modèle du monde et le moteur d’inférence et les apprendre simultanément. Il s’agit de l’objectif de notre laboratoire à Mila. Nous avons créé une structure probabiliste novatrice appelée réseaux de flot génératifs (GFlowNets ou Generative Flow Networks) pour l’inférence amortie des distributions plurimodales par rapport aux objets compositionnels. Le design des GFlowNets utilise des idées provenant de l’inférence variationnelle et de l’apprentissage par renforcement pour modéliser des objets compositionnels de façon progressive et probabiliste [Malkin et autres, 2023].
Elle a été appliquée aux domaines suivants :
- Gestion de l’incertitude et des biais dans le signal de récompense ainsi que dans les grands espaces de recherche de manière combinatoire, comme dans la découverte de médicaments [Bengio et autres, 2022; Jain et autres, 2022] et dans la planification des graphes de calcul [Zhang et autres, 2023].
- Modélisation de la distribution postérieure bayésienne par rapport aux graphes causaux qui expliquent les données d’observation et d’intervention [Deleu et autres, UAI’22].
- L’extension des algorithmes d’apprentissage automatique par échantillonnage approximatif des distributions difficiles à résoudre par rapport aux objets compositionnels. Par exemple, l’apprentissage de modèles expressifs avec variables latentes par lequel un modèle du monde est un cas spécial, en utilisant un algorithme espérance-maximisation [Hu et autres, 2023].
Si vous souhaitez en apprendre davantage sur les GFlowNets et comprendre comment ils repoussent les limites de l’apprentissage profond, vous pouvez consulter ce tutoriel.
Remerciements
Nous remercions Jacob Buckman, Chen Sun, Mo Tiwari, Donna Vakalis et Greg Yang pour leurs remarques utiles.